Лебединая песня

Согласно информации, содержащейся в книге «Развитие вычислительных машин» (Апокин И.А., Майстров Л.Е.) и всех остальных, посвященных этой теме:

умножение производилось по схеме умножения многочлена на многочлен, произведения akbn, akbn-1 и т.п. выполнялись в уме (все эти произведения в пределах таблицы умножения от 1 х 1 до 9 х 9), степени 10 указывали, на каких линиях их выкладывать, затем все эти произведения складывались (Рис.2.4.6).

Отметим, что для выполнения этих действий указанным способом необходима доска со многими вертикальными отделениями и отсутствует какой-либо ясный алгоритм по перемещению и группированию жетонов при выполнении деления.

Применяемый в данном случае счет — пятеричный. Наиболее адекватный способ отражения данного счета – греческая Геродиановская нумерация и Римские цифры, просматривается полная аналогия прибора с Саламинской доской и Римскими калькулями.

На основании изучения репринта книги «Фундамент искусств» Р.Рeкорда, и непосредственной личной практики вычислений на данном виде абака, удалось сделать несколько иные выводы об алгоритме умножения и деления, не требующем постоянного применения таблицы умножения, и сводящему необходимые действия к нескольким наглядным автоматическим операциям.

Предположим, требуется перемножить два числа: 78 и 1739.

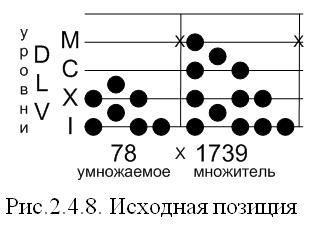Обозначим каждый уровень абака соответствующим «школьным» числом. Расположение фишек, обозначающих умножаемое назовем «фигурой».

Обратим внимание на то, что фактически любое действие умножения сводится к перемножению умножаемого числа на единицу (в количестве от 1 до 4) или на пятерку (всегда одну) множителя.

Таким образом, минимум необходимых правил состоит в следующем:

1. В случае умножения на единицы, в результате необходимо повторить фигуру умножаемого на определенном уровне (см. п. 4 ниже) столько раз, сколько единиц в множителе (в данном примере на уровне М – 1 раз, на уровне С – 2, Х – 3, I – 4 раза). При выполнении данной операции физически, жетонами, берется стопка из, соответственно 1, 2, 3 или 4х жетонов и единожды выкладывается фигура.

2. Умножение на 5 заменяется умножением на 10 (то есть, по сути, на единицу) и делением на 2. Фигура умножаемого повторяется на определенном уровне (см.п. 4 ниже) один раз и над ней производится операция деления на два.

3. После того, как эти процедуры произведены со всеми уровнями множителя, жетоны суммируются, начиная с низших разрядов, каждые 5 единиц заменяются одной пятеркой, каждые две пятерки – одной десяткой, как было описано ранее, и получается искомый окончательный результат.

4. Уровень, на котором начинает выкладываться промежуточный результат, определяется следующим образом:

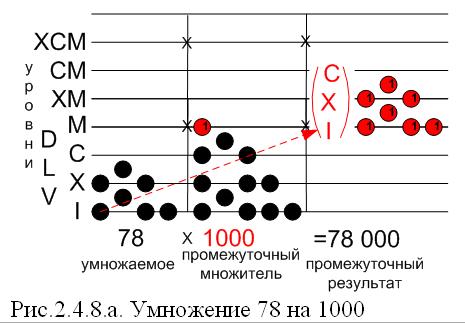
— уровень множителя берется за исходный, и на нем размещаются жетоны, принадлежащие уровню «I» умножаемого, остальные – соответственно выше, на следующих уровнях, согласно «фигуре» умножаемого.

Таким образом, в нашем примере, взяв за исходный уровень «М» нашего первого множителя 1000, отложим фигуру умножаемого, первоначально разместив на нем три жетона принадлежащие уровню «I», и далее – остальные, в соответствии с конфигурацией фигуры (Рис.2.4.8.а).
Так получим первый промежуточный результат, 78 000.

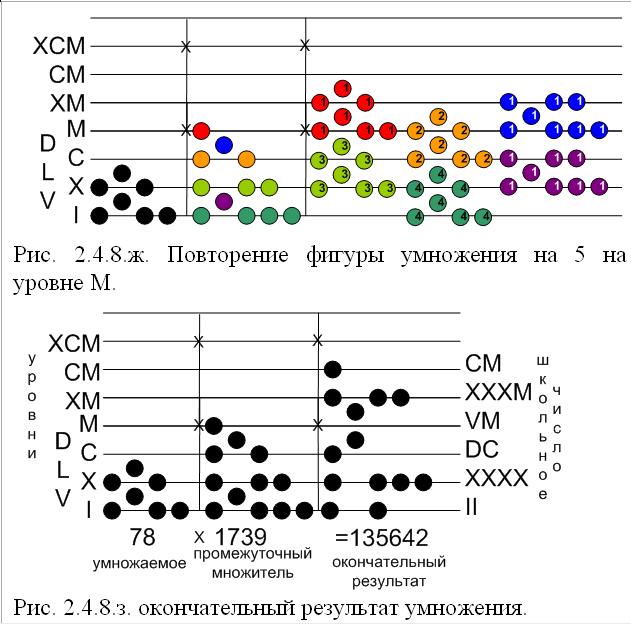
Аналогичным образом в дальнейшем повторяются фигуры для уровней С, X и I множителя:

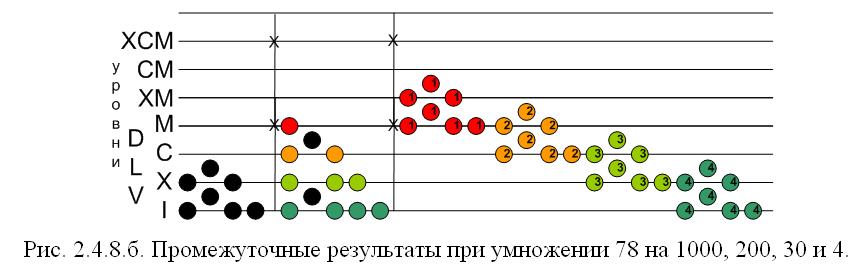
Числами на жетонах промежуточных результатов указано количество жетонов в стопке (! жетоны давали именно эту возможность — группировку в стопки), соответственно их количеству на уровне каждого промежуточного множителя.

Умножение на 5 производим умножением на 10 (позиционируя фигуру тем же способом, что и раньше) и делением на 2:

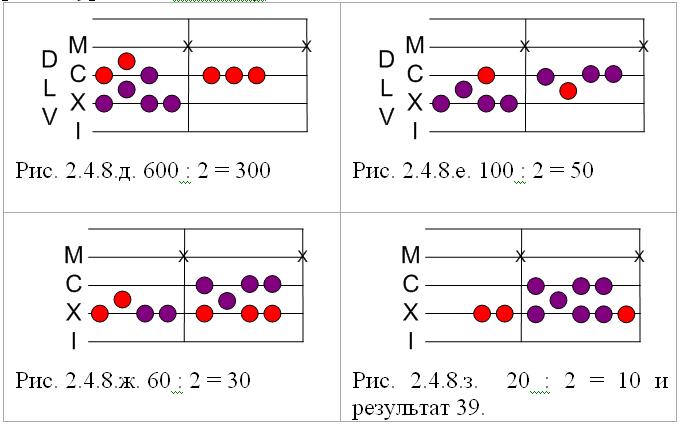
Алгоритм деления числа на число будет подробно рассмотрен далее, однако деление на 2 не вызывает трудностей путем последовательного деления пополам исходного количества жетонов начиная с верхнего уровня к нижнему.

Добавим данный промежуточный результат к предыдущему и получим:

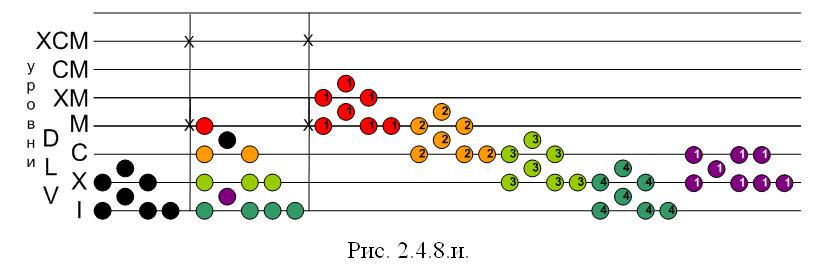Очевидно, что для умножения исходного числа на оставшийся последний промежуточный множитель 500 нет необходимости производить какие-либо вычисления, достаточно на соответствующем месте разместить фигуру результата, полученного ранее при умножении на 5 (вот где должно проявиться искусство счетчика : приемчики — это главное!!!)

Окончательный результат 135642 (CXXXVMDCXXXXII) получим предельно аккуратным суммированием всех жетонов, начиная с нижней линии вверх, как это описано ранее.

Отметим, что вопреки распространенному в литературе мнению, для умножения не требуется перемножение в уме каких-либо чисел, весь процесс сводится к перемещению в правильное место фигуры умножаемого, что является наглядным и несложным процессом и аккуратному сложению жетонов с перемещением их по мере «укрупнения» вверх по уровням. Процесс живой и наглядный. Доминирует не число — а образ, аналогия, ассоциация! (В этом и есть ключевое различие между рациональным, если хотите — дискретным мышлением современного человека и — аналоговым, ассоциативным мышлением человека средневекового!)

Отметим, что, поменяв указанные множители местами, мы сократим количество операций, то есть эффективнее умножать больший множитель на меньший (или на тот, в котором нет необходимости умножать на 5).

Далее рассмотрим самое, и по ныне, сложное действие — деление!